Solides
Reconnaître des solides (pavé droit, cube, prisme, cylindre, pyramide, cône, boule).
Savoir calculer le volume d’un prisme, d’une pyramide, d’un cylindre, d’un cône, d’une boule.
Construire et mettre en relation des représentations de ces solides (vues en perspective cavalière, de face, de dessus, sections planes, patrons, etc.).
Savoir se repérer sur une sphère.
Solides usuels
Rappels
Définitions
Un solide est une forme géométrique à trois dimensions.
Un patron d’un solide est une figure en grandeur réelle permettant de construire ce solide après découpage et pliage.
Un polyèdre est un solide dont les faces sont des polygones. Les côtés de ces polygones sont appelés arêtes, ils sont délimités par des points appelés sommets.
Méthode
Pour représenter un solide dans un plan, on peut utiliser la perspective cavalière, dans laquelle :
les arêtes parallèles et de même longueur sont représentées par des segments parallèles et de même longueur ;
les arêtes cachées sont représentées en pointillés.
Définition
Le volume est une grandeur mesurant la place qu’un solide prend dans l’espace. L’unité de référence est le mètre cube, noté m³. Il s’agit du volume d’un cube d’un mètre d’arête.
Combien de petits cubes composent le grand cube ci-dessus ?
On considère que les arêtes de ces petits cubes mesurent m. Quel est le volume du grand cube ?
Ce grand cube est composé de petits cubes.
Le volume d’un petit cube est de m³. Donc le volume du grand cube est de m³.
Définitions et volumes
Définitions
| Définition du solide | Perspective cavalière | Volume |
|---|---|---|
| Cube : polyèdre dont les faces sont des carrés. | ||
| Pavé droit : polyèdre dont les faces sont des rectangles. | ||
| Prisme droit : polyèdre qui a deux faces superposables et parallèles, et dont les autres faces sont des rectangles. | ||
| Pyramide : polyèdre qui a une base polygonale et des faces latérales triangulaires qui ont un sommet commun. | ||
| Cylindre : solide formé de deux disques parallèles (appelées bases), et d’une surface latérale correspondant à un rectangle enroulé le long de ses bases. | ||
| Cône : solide obtenu en faisant tourner un triangle rectangle autour d’un des côtés de l’angle droit. Autrement dit, un cône est un solide délimité par un disque (sa base) est une surface latérale qui représente un secteur angulaire. | ||
| Boule de centre et de rayon : un solide constitué de l’ensemble des points situés à une distance inférieure ou égale à du point . |
Calculer le volume du cube ci-dessous.
Calculer le volume du pavé droit ci-dessous.
La pyramide de Khéops est un monument construit par les Égyptiens de l’Antiquité, formant une pyramide régulière à base carrée. Un côté de cette base mesure environ m, et sa hauteur est d’environ m.

Calculer une approximation du volume de cette pyramide. Donner le résultat en m³.
L’aire de la base vaut . Donc le volume de cette pyramide est :
Une canette de cL d’un célèbre soda vendu dans le commerce peut être représenté par un cylindre de diamètre cm et de hauteur cm.
Quel volume maximal de soda peut-être contenu dans une telle cannette ? Donner le résultat en cL en arrondissant au millilitre près.
On utilise la formule pour calculer le volume d’un cylindre de rayon cm et de hauteur cm :
Calculer le volume d’un cône de rayon m et de hauteur dm.
Il faut convertir la hauteur du cône en mètres : . On peut maintenant utiliser la formule :
Calculer une approximation du volume d’une boule de pétanque de diamètre mm.
On utilise la formule pour calculer le volume d’une boule.
Sections planes
Définition
On appelle section d’un solide par un plan l’intersection de ce solide avec ce plan.
Propriétés
La section d’un pavé droit par un plan parallèle à l’une de ses faces est un rectangle de même dimension que cette face.
La section d’un cylindre par un plan parallèle à sa base est un disque de même rayon que la base.
La section d’un cylindre par un plan perpendiculaire à l’une de ses bases est un rectangle dont l’une des dimensions est la hauteur du cylindre.
La section d’une pyramide ou d’un cône par un plan parallèle à sa base est une réduction de la base.
La section d’une sphère par un plan est un cercle.
On a coupé une sphère de centre et de rayon cm par le plan représenté ci-dessous.
On a obtenu un cercle de centre passant par le point de la sphère et tel que cm. Quel est le rayon de ce cercle ? Arrondir le résultat au millimètre près.
Le triangle est rectangle en , on peut appliquer le théorème de Pythagore. D’où : Donc : Le rayon de ce cercle est donc d’environ cm.
Repérage sur la sphère
Définitions
Sur une sphère, on peut se repérer à l’aide de grands cercles. Il s’agit de cercles tracés à la surface qui ont le même diamètre qu’elle et qui la divisent en deux hémisphères égaux.
Sur notre planète (assimilée à une sphère), ces grands cercles sont des méridiens et des parallèles.
La latitude exprime la position Est-Ouest par rapport au méridien de Greenwich.
La longitude exprime la position Nord-Sud par rapport à l’Équateur.
On considère le globe terrestre ci-dessous.
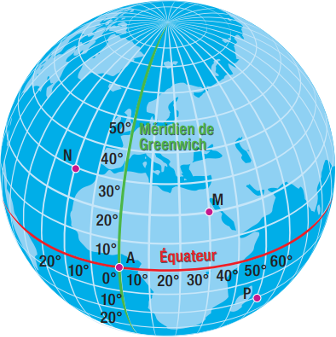
Lire les coordonnées géographiques des points , et (ie. leur latitude et leur longitude).
:
:
:
: .
: .
: .











